This week in MathOnco 163

Bayesian frameworks, ecological hallmarks, optimal control, agent-based modeling, and more!

“This week in Mathematical Oncology” — Newsletter

May. 20, 2021
>jeffrey.west@moffitt.org

From the editor:


Summary of contents:

Today’s issue contains a ton of exciting math oncology work. Be sure to scroll down to check out the cover artwork (designed by Stefano Pasetto & Heiko Enderling), and don’t miss the upcoming PhysiCell workshop.

• Enjoy,
-Jeffrey West

1. Bayesian Framework to Augment Tumor Board Decision Making
   Stefano Pasetto, Robert A. Gatenby, Heiko Enderling

2. Learning differential equation models from stochastic agent-based model simulations
   John T. Nardini, Ruth E. Baker, Matthew J. Simpson, Kevin B. Flores

3. Cancer immunoediting: A game theoretical approach
   Fatemeh Tavakolia, Javad Salimi Sartakhtib, Mohammad Hossein Manshaeia, David Basanta

4. Modeling historic incidence trends implies early field cancerization in esophageal squamous cell carcinoma
   Georg E. Luebeck, Thomas L. Vaughan, Kit Curtius, William D. Hazelton

5. Applying symmetries of elasticities in matrix population models
   Stefano Giaimo, Arne Traulsen

6. The Hallmarks of Cancer as Ecologically Driven Phenotypes
   Jason A. Somarelli

7. Ten steps to investigate a cellular system with mathematical modeling
   Jasia King, Kerbaï Saïd Eroumé, Roman Truckenmüller, Stefan Giselbrecht, Ann E. Cowan, Leslie Loew, Aurélie Carlier
   

1. Implementation and acceleration of optimal control for systems biology
   Jesse A Sharp, Kevin Burrage, Matthew J Simpson

2. Mathematical modeling quantifies ERK-activity in response to inhibition of the BRAFV600E-MEK-ERK cascade
   Sara Hamis, Yury Kapelyukh, Aileen McLaren, Colin J. Henderson, C. Roland Wolf, Mark A.J. Chaplain
   

1. 2021 PhysiCell Workshop and Hackathon
Paul Macklin is organizing a virtual workshop and hackathon July 25-31 on multiscale cancer modeling using PhysiCell—an open source agent-based modeling platform. Participants will learn to build agent-based models of cancer in diffusion-driven microenvironments, integrate intracellular signaling models, share models as cloud-hosted web apps, and compete in a hackathon. Tutorial sessions are open to the public and streamed, while the afternoon hackathon is reserved for up to 30 participants, who will receive a $1500 honorarium (and PhysiCell swag!) For fullest consideration, apply by May 31, 2021 at http://PhysiCell.org/ws2021. Follow @PhysiCell (Twitter) and @get.PhysiCell (Instagram) for details.

2. Can we use ecological principles to understand — and perhaps treat — cancer?
Written by: Gunnar De Winter
"The author begins by noting that cancer cells are a distinct population of cells that find themselves within an ecosystem of other cells/tissue (our bodies). Within that ecosystem, cancer cells try to do what most organisms try: survive and reproduce. To achieve this, cancer cells have to interact with their environment as well as evolve possible ways to face challenges such as the immune system. A successful cancer does this by responding swiftly to selective pressures. Tumor cells evolve to forage (seek out nutrients or reroute nutrient supplies), avoid predation (by the immune system), migrate (find new, possible better places to take root), and reproduce. Sounds a lot like a population of animals, doesn’t it?"

The newsletter now has a dedicated homepage (thisweekmathonco.substack.com), which allows us to post cover artwork for each issue. We encourage submissions that coincide with the release of a recent paper from your group. Today’s submission is below:

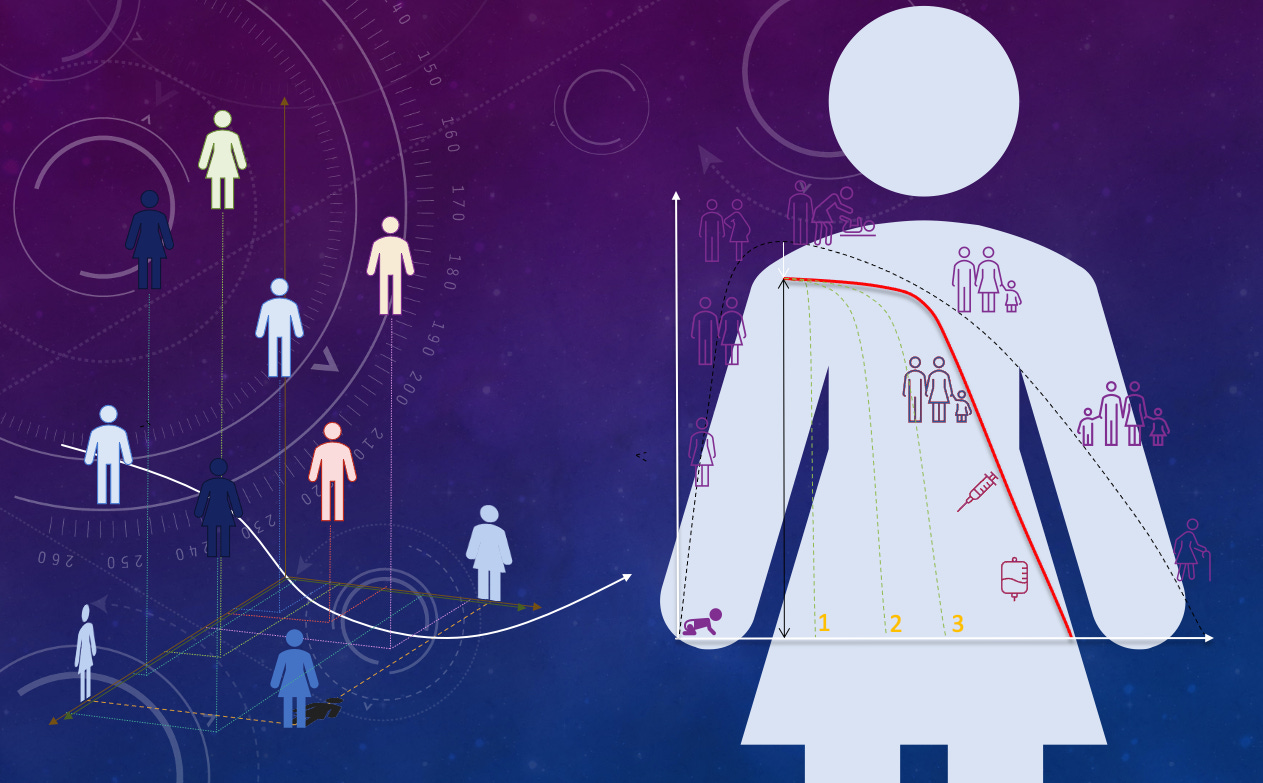
Caption: “Mathematical modeling of an oncological treatment starts with defining a precise reference frame where locating the considered patients’ biomarker values (left part of the figure). By considering patient anamnesis and present condition, the role of the model is then to forecast the treatment evolution in that framework to help identify the optimal treatment (right part of the figure).” 

Created by Stefano Pasetto & Heiko Enderling, submitted in conjunction with their recent publication, found here.

• Networks in Cancer: From Symmetry Breaking to Targeted Therapy
  Guest Editor: Cristian Axenie, Roman Bauer, María Rodríguez Martínez

• Understanding the Evolutionary Dynamics and Ecology of Cancer in Treatment Resistance
  Guest Editor: David Basanta

• From Ecology to Cancer Biology and Back Again
  Guest Editors: Fred Adler, Sarah Amend, Chris Whelan

• Frontiers in quantitative cancer modeling
  Guest Editors: Mohit Kumar Jolly, Heiko Enderling

• NEW: Assistant Professors in Mathematics (Morten Andersen)

• Senior Quantitative Systems Pharmacologist, Pfizer Oncology (Blerta Shtylla)

• Mathematical Immuno-Oncology postdoc (Kasia Rejniak, Moffitt)

• Research Fellow in Computational Systems Biology Cancer Research (Simon Mitchell)

• PhD student - Measuring cancer evolution in a changing tumour microenvironment (Xiaowei Jiang)

• Postdoctoral Scholar - Genetics and Genome Sciences (Christopher McFarland)

• Postdoc on colorectal cancer evolution or cancer immunotherapy (Ivana Bozic)

• Postdoc on cancer/immune modeling and machine learning (Eduardo Sontag)

• PhD candidate/Early Career Researcher: Theory of Stackelberg evolutionary games for cancer treatment (Katerina Stankova)

• Early Stage Researcher: Impact of different resistance mechanisms on the outcomes of cancer treatment game (Weini Huang)

• Early Stage Researcher: Evolutionary therapy in ovarian cancer (Ben Werner)

• CDC Steven M. Teutsch Prevention Effectiveness Fellowship

• Mathematical Modeling Expert in Oncology Translational Science (Boehringer Ingelheim)

• Research Associate - Biostatistician (University of Manchester)

• Director Quantitative Clinical Pharmacology, Oncology

• Principal Scientist – Oncology PK/PD Modelling (Boehringer Ingelheim)

• Biosimulation Scientist (Physiomics)

• Postdoctoral Research Position in Computational Immunology (Sylvain Cussat-Blanc)

• Systems Biology Modeler Positions in Biopharma Consulting Company (Helen Moore)

• Computational Approaches to Breast Cancer Evolution - Postdoc (Marc Ryser)

• Math/statistical models of stem cell lineage dynamics and cancer genomics - Postdoc (Adam MacLean)

• Machine Learning / Math Modeling Postdoc (Noemi Andor)

• Cancer immunotherapy / systems bio postdoc (Elana J Fertig)

• Integrated Math Oncology Ph.D. (Moffitt)

• Integrated Math Oncology Postdoc (Sandy Anderson)

• Postdoctoral Research Position in Computational Oncology (Tom Yankeelov)

Current subscriber count: 950